

I can post an equation up later (I should be studying right now), so in the mean time you might want to read up on differential equations. To get your answer you have to solve a differential equation, not an integral. None of us have regurgitated an equation because there isn't a simple one. Unfortunately you can't use d =v 1t +1/2 at 2 because it assumes constant acceleration which, as you noticed, you do not have. I'm still reading through and trying to understand.Īnd disappointed not one of you has regurgitated an equation for me to use.

I've come up with MU/R^2*mass which will give you the thrust to cancel out acceleration from gravity, i.e you will decend (or even ascend) at a constant speed. The forces are a necessary nastiness of doing this properly, right? I'm pretty lost at this point, but all I want is given a thrust value, a distance to stop within. I've figured out it's the integral (area in non-stupid terms) of F=GMm/R^2, combined with something like d =v1t +1/2 at^2?. land without crashing at a bajillion km/hr? Right, but since F = GMm/R^2 changes (because of the R) as you descend, how do you figure out at what altitude to thrust at to get to 0 velocity at a particular value of R. Hope this helps, please ask if I'm not clear on anything. If you want to find the acceleration due to gravity at any given point, assuming that it is falling directly straight down with no other forces acting on it, then you can use your second equation to work out the force due to gravity and then the first equation to work out how much that is going to accelerate it. It then changes the velocity of the ship based on this force, and the acceleration is just the difference between the new speed and the old speed divided by the time between the time-steps.
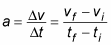
KSP doesn't really use either of these. Being a computer it solves things numerically, so (and this is a pretty huge simplification, possible not 100% accurate to the way it's implemented in KSP) at each time-step (roughly once per frame, but not necessarily) it calculates the force on he ship due to the gravitational body that the ship is in the SOI of.
PHYSICS CALCULATOR ACCELERATION CODE
I could test this using kOS and writing a bunch of code to measure it, but for the moment, it seems easier and quicker to ask here. I'm guessing they meant it's 2-body when calculating the physics for ships? I've heard ksp is a 2-body system, but in that case it's really 1-body. Those are all 'on-rails' or fixed/nerfed to defy the exact laws of physics though (in order to implement the scaling). I have already painstakenly determined that for moons orbiting other planets, it does not use the second mass to implement the orbital characteristics. Ideally on a body with no atmospheric drag. And no, I'm not asking about rocket thrust, for which I know it (roughly) does account for, I'm simply talking about a free-falling object. Which one does ksp use to determine velocity/acceleration? i.e.

It's well known that F=m*a, and perhaps lesser well known that F = G*M1*M2/R^2.


 0 kommentar(er)
0 kommentar(er)
